Les données de WMAP ont joué un rôle essentiel en établissant le modèle standard de l’univers. Ce modèle explique aujourd’hui un grand ensemble de mesures cosmologiques et astronomiques effectuées sur un grand domaine de longueurs d’onde et d’outils d’observation : anisotropies du CMB, abundance des éléments légers, observations des grandes structures (LSS) et propriétés des amas de galaxies, mesures de la constante de Hubble, accélération de l’expansion d’univers mesurée par les supernovae, et d’autres mesures. La concordance de ces données implique que notre univers est plat, avec des perturbations cosmologiques décrites par la théorie de relativité générale d’Einstein dans trois dimensions spatiales. Notre univers est actuellement dominé par l’énergie noire (72%) équivalente à une constante cosmologique, complétée par de la matière noire (environ 23.4 %), et des atomes (4.6 %), avec des fluctuations de densité engendrées par un processus initial gaussien, invariant d’échelle, et adiabatique (inflation). L’énergie noire agit comme une forme d’anti-gravité et est responsable de l’accélération actuelle de l’expansion de l’univers. La matière noire est différente des atomes, n’émet pas de lumière et elle n’est détectée que par gravité. L’inflation est l’étape primordiale de l’expansion accélérée de l’univers, dans laquelle sa taille croît d’un facteur 1026. L’inflation dure approximativement 10-34 secondes et se termine au redshift 1028.
Les fluctuations du CMB sont expliquées par l’inflation et le modèle de concordance. Les fluctuations quantiques microscopiques à l’échelle de l’inflation de 10-27 cm evoluent en fluctuations macroscopiques aujourd’hui, aux échelles de 1000 Mpc = 1027 cm. Une telle transition entre fluctuations microscopiques et macroscopiques est le caractère propre de l’inflation.
L’inflation est décrite par un champ scalaire (l’inflaton) qui controle la dynamique du facteur d’échelle de l’univers. L’inflation résoud des problèmes importants de la théorie standard du Big-Bang, et fournit un mécanisme générique pour engendrer des perturbations scalaires (densité) et tensorielles (onde gravitationelle) .
Les ondes gravitationelles primordiales sont une prévision robuste de l’inflation car elles sont produites par le même mécanisme qui a produit les fluctuations primordiales de densité observées dans les données du fond cosmologique (CMB) et des grandes structures (LSS). Récemment, l’équipe a effectué une nouvelle analyse avec MCMC (Monte Carlo et chaînes de Markov) de toutes les données disponibles du CMB et des LSS comprenant les données de WMAP et Sloan. Cette nouvelle analyse est réalisée dans la nouvelle approche de l’inflation comme théorie efficace dans l’esprit de Ginsburg-Landau, i.e. avec des potentiels trinomials du quatrième degré dans le champ d’inflaton. L’approche de Ginsburg-Landau est un outil puissant dans la physique de particules élémentaires (physique des mésons pi) et la physique de la matière condensée (superconductivité et transitions de phase). Dans cette nouvelle analyse, la forme précise du potentiel inflationaire est construite en ajustant les données de WMAP et de LSS.

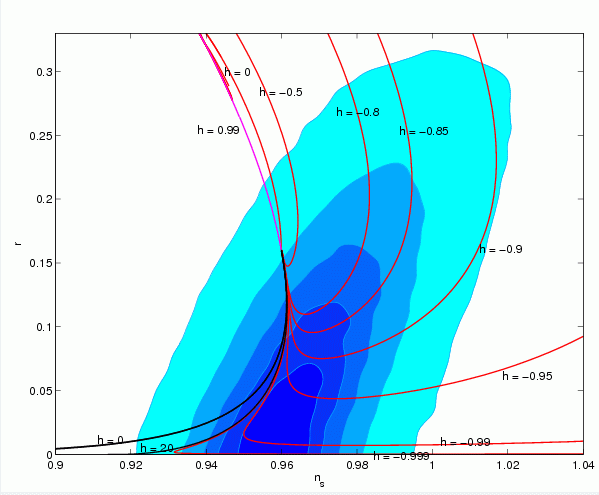
L’équipe dérive des formules explicites pour les observables de CMB et les étudie : l’indice spectral ns des fluctuations de densité, le rapport r des fluctuations tensorielles/ scalaires, et l’indice courant d ns/dln k . Ces formules analytiques ont été présentées en tant que contraintes dures sur ns et r dans le programme numérique de l’analyse MCMC. Cette analyse de données diffère dans cet aspect crucial de toutes les analyses de données précédentes, en particulier de l’analyse de l’équipe WMAP (mars 2008).
Dans le cadre de leur modèle, les nouveaux résultats de l’équipe sont les suivants :
- Les données indiquent fortement la brisure (spontanée ou explicite) de la symétrie des potentiels d’inflation.
- Le potentiel trinomial d’inflaton avec deux minima (c’est à dire le puits de potentiel double) répond naturellement à cette exigence et fournit le meilleur ajustement aux données
- Le potentiel symétrique d’inflaton avec seulement un minimum (potentiel avec le terme quadratique positif) est presque certainement éliminé (au CL de 95%)
- Le potentiel trinomial préféré d’inflation est un double puits, fonction paire du champ avec un couplage quartique modéré y avec les valeurs les plus probables : ns 0.958 r 0.055 . Cette valeur de r est à la portée des prochaines observations du CMB
Une limite inférieure pour r est trouvée : 0.016 (95% CL) and 0.049 (68% CL). Ceci prouve que la quantité de fluctuations tensorielles (ondes gravitationelles primordiales) est non nulle, dans ce modèle. C’est un résultat important car jusqu’à présent seulement des limites supérieures pour r ont été trouvées, la dernière étant r < 0.20 (CL de 95%). De plus, la limite inférieure sur r sera encore précisée avec l’utilisation de WMAP 5 et les prochaines données du CMB.
Références
- [1] "MCMC analysis of WMAP and SDSS data points to broken symmetry inflaton potentials and provides a lower bound on the tensor to scalar ratio" C. Destri, H. J. de Vega, N. G. Sanchez, Phys. Rev. D 77, 043509 (2008)
- [2] "New Inflation vs. Chaotic Inflation, Higher Degree Potentials and the Reconstruction Program in light of WMAP3" D. Boyanovsky H. J. de Vega, C. M. Ho, N. G. Sanchez, Phys. Rev. D 75, 123504 (2007)
- [3] "Clarifying Inflation Models : Slow-roll as an expansion in 1/Nefolds and No Fine Tuning", D. Boyanovsky, D. Boyanovsky, H. J. de Vega, N. G. Sanchez, Phys. Rev. D 73, 023008 (2006).
- [4] "Single Field Inflation models allowed and ruled out by the three years WMAP data", H. J. de Vega, N . G. Sanchez , Phys. Rev. D 74, 063519 (2006).
Contact
- Norma Sanchez
(Observatoire de Paris, LERMA, et CNRS)
