Les halos de matière noire sont les pierres fondamentales de la formation de structures dans l’univers. Ils sont constitués de particules de matière noire liées par la gravité, et à l’intérieur des halos la matière baryonique sous forme de gaz se refroidit et s’effondre pour former les étoiles et les galaxies que nous observons aujourd’hui. Les plus grands de ces halos dans l’univers accueillent des amas de galaxies (M=1015 Msol), alors que les plus petits peuvent héberger des galaxies naines (M=108 Msol) et constituent une population de petites structures satellites qui orbitent autour des galaxies comme la Voie Lactée. La gamme de masse de ces halos couvre plusieurs ordres de grandeur. Quelle est l’abondance de ces objets ? Comment sont ils distribués dans l’univers ? Est-ce que leurs caractéristiques évoluent au fil des milliards d’années ? Grâce aux progrès numériques des dix dernières années, les scientifiques ont tenté de répondre à ces questions à l’aide des simulations numériques à N-corps sur les ordinateurs les plus performants au monde. Ils ont étudié la complexité du processus de formation des halos, causé par l’interaction gravitationnelle en régime fortement non linéaire (figure 1). Cependant une étude théorique fiable reproduisant les propriétés de la distribution de la masse de ces halos n’avaient pas été proposée.

Pier Stefano Corasaniti cosmologue au LUTh et Ixandra Achitouv doctorante à l’université de Paris Diderot ont réussi à calculer la fonction de masse de ces halos de matière noire avec un accord sans précédent avec celle mesurée dans les simulations numériques N-corps. Leurs travaux s’appuient sur une formulation stochastique de la formation des halos. L’idée étant de lier la distribution en masse de ces halos aux propriétés statistiques du champ de matière primordial observé par l’intermédiaire des anisotropies du fond diffus cosmologique. Le lien est réalisé grâce à un processus de filtrage du champ de densité primordial sur différentes échelles de longueur. Le filtrage permet ainsi de définir divers volumes auxquels on associe la masse des différents halos. Le processus de formation d’un halo est alors représenté par une marche aléatoire du champ de densité en fonction de l’échelle caractéristique de filtrage. Un halo se forme lorsqu’il dépasse un seuil critique d’effondrement (figure 2). Le calcul de la distribution de masse dans les halos se réduit alors au comptage des marches aléatoires qui dépassent ce seuil en fonction de l’échelle du filtre (ou de la masse associée). En effet, une prédiction théorique de la formation de chaque halo à partir de la distribution spatiale du champ de densité initial de la matière noire dans tout l’univers reste inenvisageable. En revanche, prédire les propriétés statistiques de la distribution de masse des halos est un défi plus abordable. Surtout si on considère que ces propriétés moyennées peuvent être confrontées directement aux observations comme celles de l’abondance d’amas de galaxies massives.

Figure 2 : Marche aléatoire de la perturbation de densité en fonction de la variance du champ de densité à différentes échelles de filtrage Cliquer sur l’image pour l’agrandir Richard Bond, Shaun Cole, George Efstathiou et Nick Kaiser sont les pères du modèle stochastique appliqué à la formation de halos. Ce modèle développé au début des années 90 est connu sous le nom d’ « excursion set theory ». Néanmoins la résolution analytique n’a pu être faite que sous certaines hypothèses qui ne sont pas physiques, entre autres la définition de la masse. Utiliser une bonne définition de la masse qui soit en concordance avec l’observation se traduit mathématiquement par des corrélations dans l’étude des trajectoires. Le comportement d’une trajectoire dépend alors de son histoire passée ce qui complique énormément la prédiction. C’est comme si les prix du marché financier progressaient lentement suivant une loi déterministe au lieu de faire des sauts aléatoires car les investisseurs se seraient concertés au préalable. Pour formaliser ce problème et le résoudre, les théoriciens ont introduit l’outil d’intégrale de chemin. L’intégrale de chemin a été développée dans un tout autre contexte qui est la théorie quantique des champs. Cet outil permet de construire la probabilité de transition d’un point à un autre en passant par tous les chemins intermédiaires possibles du processus aléatoire. Récemment, Michele Maggiore, professeur à l’Université de Genève et Antonio Riotto chercheur au CERN, ont réussi à formuler l’ « excursion set theory » à l’aide d’intégrales de chemin et ont ainsi résolu de manière formelle le problème de corrélation entres les trajectoires. C’est avec ce formalisme que les théoriciens du LUTh ont effectué leur calcul. Cependant, ils ont eu l’idée d’améliorer la description du seuil de formation des halos. Dans les modèles précédant ce seuil était déterminé dans un cas très idéal où le collapse était sphérique et découplé du resde l’univers. Cela est une bonne approximation seulement pour les halos des très grand masse qui se forment sur les très grandes échelles de façon presque isolée. En effet, l’environnement joue un rôle important dans l’évolution de la surdensité tout particulièrement aux petites échelles. Ceci tend à changer la condition de collapse suivant l’échelle. Pour rendre compte de ces effets il faut considérer le modèle de collapse ellipsoïdal. Les chercheurs ont réussi à implémenter cet effet grâce à une modélisation stochastique de la barrière qui dépend de l’échelle. Le résultat de leur travail est une fonction de masse qui dépend de paramètres physiques liés au collapse gravitationnel permettant ainsi de comprendre les caractéristiques liées à sa forme, sur toute la gamme de masse sondée par les simulations numériques. Par ailleurs, leur fonction de masse reproduit avec un très haut degré de précision ce qui a été mesuré dans les simulations numériques (figure3).
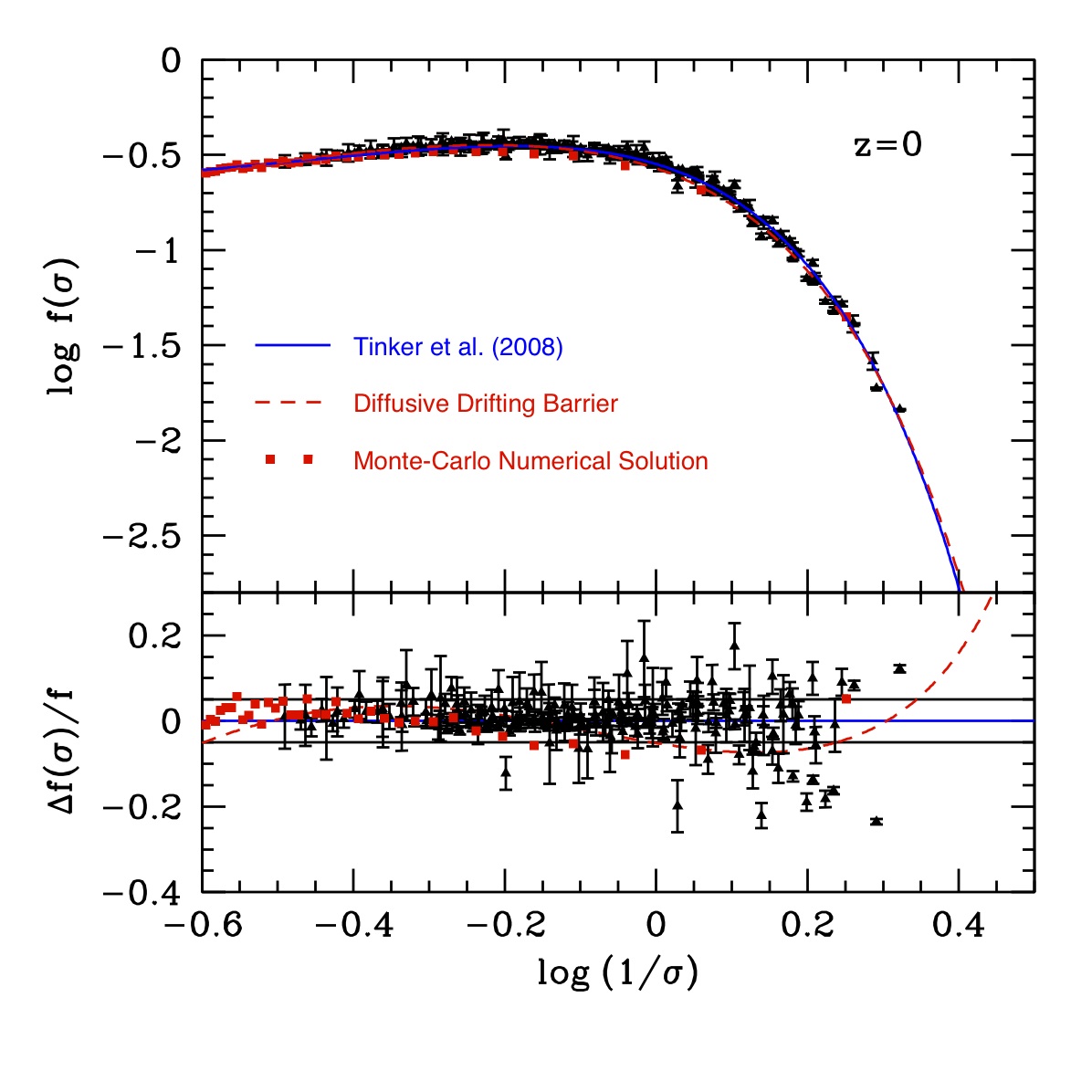
Selon les deux chercheurs cette étude est le commencement d’une toute nouvelle approche permettant de décrire la fonction de masse des halos de matière noire. Leurs travaux ont ouvert de nouvelles voies de recherche. Entre autres la généralisation au cas où la statistique du champ de densité initiale change selon différents modèles de physique des hautes énergies. En effet, certains modèles de théories des cordes prédisent différentes corrélations entre les perturbations du champ de matière après le Big Bang. D’autre part, leur modèle stochastique du seuil de formation des halos peut être amélioré et permettre ainsi une étude sur l’influence des différents types d’univers sur les paramètres de collapse qui décrivent la formation des halos. Les travaux effectués au LUTh ont prouvé d’une part qu’une compréhension théorique des propriétés des halos engendrés à partir de phénomènes gravitationnels complexes est possible et d’autre part que ces propriétés sont prédictives grâce à leur modélisation.
[1] P.S. Corasaniti and I. Achitouv, Phys. Rev. Lett. 106 (2011) 241302
[2] P.S. Corasaniti and I. Achitouv, Phys. Rev. D in press.
